Анализ поведения функции

Летальность от ковида по Петербургу в качестве примера я выбрала, потому что она меньше всего прыгает и самая загадочная.
Вот такая она:

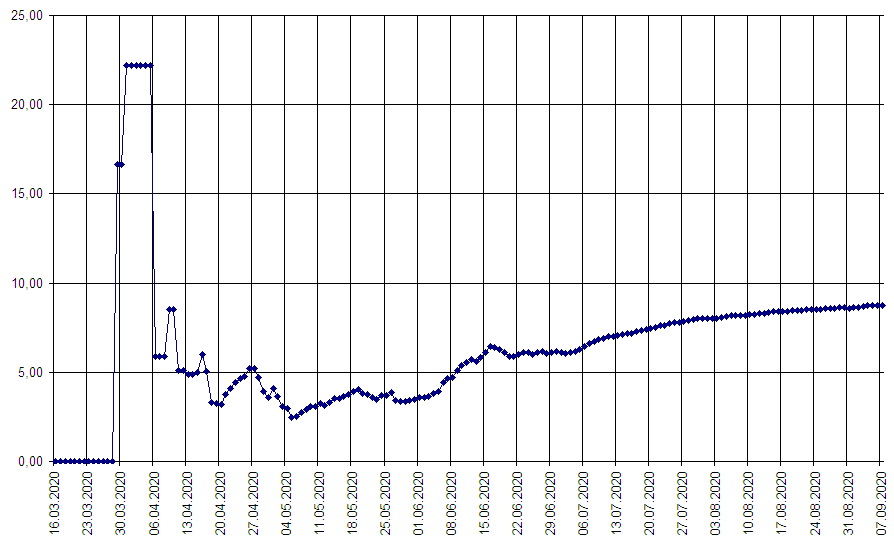
Реальность попадает в учебники очень поздно. На начальных стадиях исследования это всегда набор каких-то экспериментальных данных. Поведение реальности уже зафиксировали, но пока нет даже намека на объяснение, почему происходит так.
Смотрю я на этот график и очень мне хочется срезать начальный период до 6 апреля. И срежу. Потому что, что хочу, то и делаю))). Но. всё-таки, обосную действие. Когда вводится гипотеза сплошной среды, определятся малый объем материи (газа или твердого предмета). Но этот малый объем должен быть достаточно большим, чтобы не пришлось учитывать случайные хаотические движения двух – трёх молекул, которые в нём летают. На этом уровне малости объемов всё совсем другое.
Так и тут, есть у меня ощущение. что начальные скачки от нуля до 20 процентов вызваны случайными свойствами здоровья первого десятка заболевших. Это тоже может быть интересно (также как отдельный курс статистической физики), но сейчас я этим заниматься не хочу. Итак, выбрасываю этот начальный период и вижу такое:

А теперь попытаюсь описать то, что я вижу. Итак:
1] Все значения функции за указанный период находятся в диапазоне от 2 до 9
2] Можно сказать, что функция убывает до 5 мая, а с этого числа начинается её стабильный рост.
3] Минимальное значение функции достигается 5 мая
4] Рост функции продолжается, что позволяет предположить, что 10% будет. Но этот рост замедляется, пока не давая повода предположить 20 и больше процентов в конце процесса.
5] У функции есть множество точек, где резкий рост сменяется резким спадом и наоборот.
6]  У функции есть несколько относительно гладких периодов (подчёркнуты красным), т.е периодов некоторой стабильности ситуации. Интересно, что все они на поздней стадии процесса, а самый длительный сейчас.
7] Летальность стабильно растёт с 3 июля.
Что тут ещё можно добавить? Наверное, то, что никого закона, объясняющего происходящее, я не сформулирую ни сразу, ни чуть подумав. И то, что обилие экспериментальных данных позволяет увидеть целую функцию а не отдельные точки.
С пиками максимумов и минимумов всё, более – менее, понятно. Можно аккуратно зафиксировать даты этих пиков и достигнутые в них значения.
Рост и убывание функции тоже легко увидеть на графике. Но неплохо бы завести какой-то количественный показатель, чтобы была возможность сравнивать где рост больше а где меньше.
Теоретически всё просто. Рост и спад логично мерить в углах наклона:

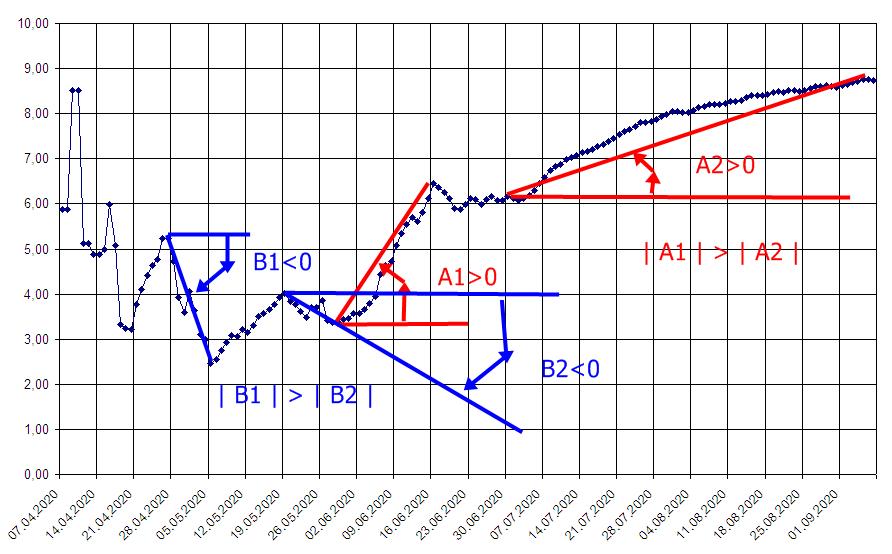
Положительное значение углов будет при росте функции, отрицательное при уменьшении. Чем больше наклон, том больше модуль угла (модуль положительного числа – само число, модуль отрицательного числа – оно же без минуса).
Но тут возникает… избыточность информации, вместе с неточностью и сложностью. Зачем знать, сколько там сложно считаемых градусов, которых 90 только потому, что в году 365 дней?
Я могу растянуть чуть-чуть картинку и все углы наклона изменяться. Так что величина угла зависит от размера бумаги.
А меня один график. Я не собираюсь сравнивать его изменения с ещё чем-то в других задачах. Самое простое, что я могу сделать, чтобы понять увеличился рост функции или уменьшился (в сравнении с другим периодом), это просто сравнить значения в соседних точках в двух этих периодах. Точнее вычесть значения функций в соседних точках (сравниваемых периодов) и сравнить полученные разности. 
Если периоды, за которое шёл, например, рост, одинаковые, то и этого достаточно. А если они разные, то сравнивать логично «погонный» рост, т.е полученные разности величин, делённые на период происходящего.
Полученная величина – с одной стороны – тангенс угла наклона функции (по которому при желании можно сразу узнать угол), а с другой – определение первой производной.
Довольно часто про первую производную функции говорят, что это - скорость. Да… в конкретных задачах и на конкретных графиках. Но сам инструмент – функция, может и возник в физике Ньютона, но довольно давно вышел за её пределы.
Потому название «производная функции», т.е нечто, посчитанное по значениям функции, подходит лучше. От себя добавлю только что придуманный «погонный спад/рост», т.е рост (спад) делённый на то, что по оси X/
Считается первая производная так:

Все обозначения производных в данном случае равносильны. f – функция от единственной переменной x, потому без разницы, которое  «d» писать.
Штрих – ещё одно обозначение производной. Не люблю его. Писать просто. Но увидеть сложно и потерять при перезаписи вычислений просто.
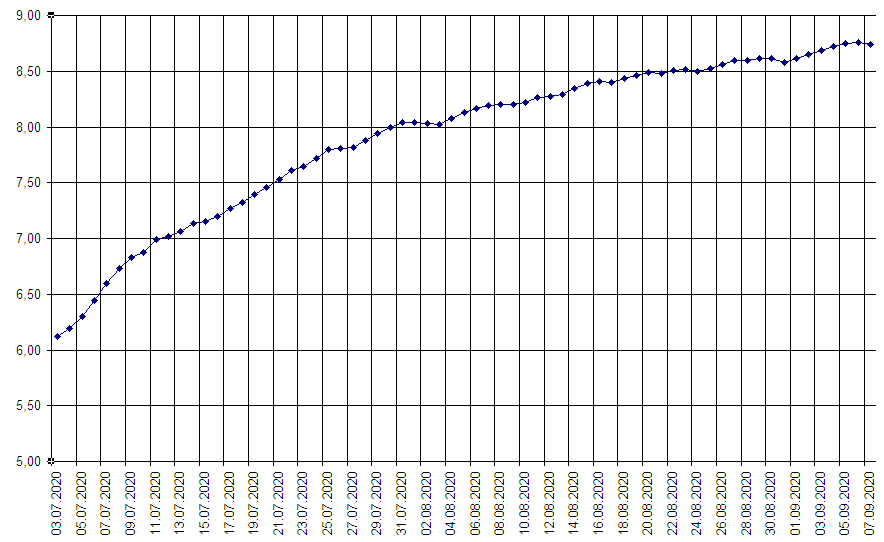
Конкретного вида гладкой функции, полученной из кого-то «ковидного закона», у меня нет. Но значения производной я запросто могу посчитать и по экспериментальным данным: Только я ещё сокращу период, потому что я хочу повнимательнее посмотреть на период стабильного роста (с 3 июля):
Так выглядит функция летальности за этот период:

А так её первая производная:

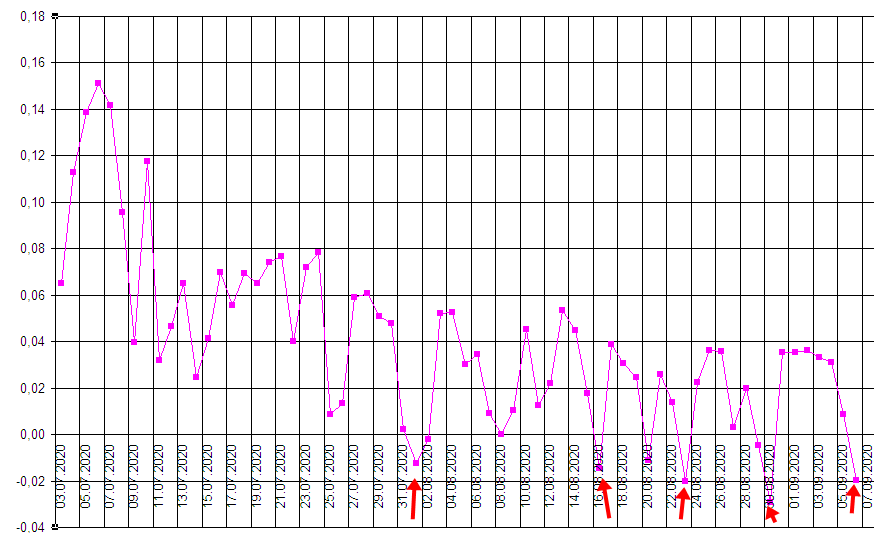
Первое, что, по-моему, бросается в глаза это то, что производная – намного более чувствительный инструмент. Довольно гладкая функция сверху и вот какие скачки производной снизу.
По графику производной я вижу, что наибольший рост был вначале. Это я, впрочем, вижу и по основному графику летальности.
А ещё я вижу, что 1 августа ситуация первый раз переломлена. Рост летальности, хоть и ненадолго сменяется спадом (а первая производная становится отрицательной). С этого момента такие дни следуют один за другим.
Можно посчитать и вторую производную. Чтобы посчитать вторую производную с первой производной надо сделать то же, что сделано с исходной функцией:

Я тут не делю приращения функций на приращение аргумента. Во-первых, я не знаю, делить мне на 1 день или на 24 часа. Во-вторых, для понимания происходящего мне и так хорошо.
А теперь я возьму период с 3 июля (начало стабильности) по тот самый переломный момент 1 августа. Основная функция летальности на этом периоде выглядит так:

По ней видно, что некоторый намёк на рост роста был только в самом начале. Потом были колебания вверх вниз, но не тенденция.
Первая и вторая производные на этом периоде выглядят так:

В самом начале графика очень большая первая производная, т.е большой рост функции (относительно последующих в этом периоде стабильности).
Вторая производная на том же начальном этапе положительна. Но она убывает. Значит, убывает скорость роста.
На исходом графике не видно, что происходит в его 4-й точке. Первая производная в этой точке достигает максимума и начинает уменьшаться. А поведение второй производной (т.е её уменьшение) позволяет чуть раньше предсказать, что так случится. Снижение скорости роста скорее всего приведёт к спаду через некоторое время.
Курс математического анализа ассоциируется с пределами, производными и интегралами. Там много чего, наверное, но на выходе в первую очередь этот набор инструментов.
Производные только что описаны.
Пределы тоже, на самом деле, уже упомянуты, только не названы. Первый вопрос, который возникает если посмотреть на функцию – «Какая летальность будет, когда всё закончится?». Это поведение функции на бесконечности, т.е в достаточно удалённой временной точке.
Здесь:
https://akostina76.ucoz.ru/blog/2020-09-06-6727

… я попыталась интерполировать квадратными и прочими корнями из Х, просто потому, что эти функции по виду больше похожи на то, что получено в эксперименте.
На самом деле, так тоже нельзя делать, потому что все эти функции тоже уходят на бесконечность, хоть и намного медленнее:
http://matematikam.ru/calculate-online/predel-limit.php

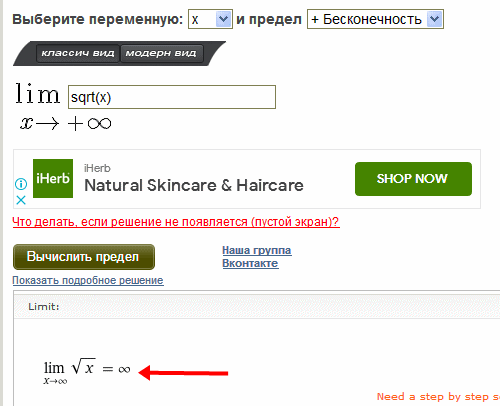
По виду функции вот так сразу и не скажешь. Но можно доказать математически точно, что и эта функция уйдут на бесконечность, и даже не на 100 процентов спирта.
Что касается интегралов, то это – площадь под графиком по какому-то диапазону X:

На картинке – смертность от ковида в мире. Смертность от Испанки в 1918-м году впечатляет намного больше. Но если приглядеться, что видно что вторая волна – пологая, но померло от ней уже сейчас, похоже больше, чем от первой. Точное значение по экспериментальным данным считается простым суммированием. А чтобы посчитать его по гладкой заданной функции надо уметь считать интеграл от этой функции.
Определённые интегралы, т.е не функции, а вычисленные значения площадей, тоже ставят в первую очередь вопросы предельных значений. Если я просуммирую значении функции от минус до плюс бесконечности, оно у меня случайно бесконечным не станет?  Просто от умножения не важно чего  на целых две  бесконечности?
По-разному бывает. Площадь под такой функцией:

… которая выглядит так:

… и значения которой на бесконечностях бесконечно малы, но нулю, всё-таки, не равны – конечна:

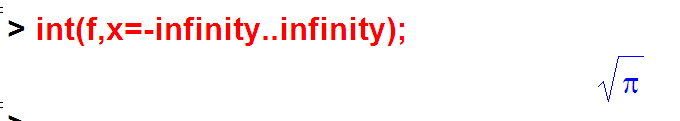
… и равна тому самому корню из ПИ, который возникает в функции нормального распределения:
https://akostina76.ucoz.ru/blog/2019-04-10-5772

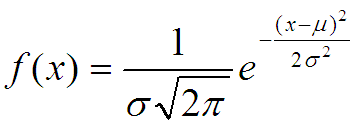
… и благодаря которому сумма вероятностей становится интуитивно понятной единицей, а не довольно странным корнем из ПИ, как должно быть при суммирование площади под графиком такой функции.
Чтобы получить этот несчастный корень из ПИ (значение интеграла – площади) очень много чего нагородить надо и про предельные значения функцией и про бесконечные суммы бесконечно малых и про всё остальное.