Демократия и множества

Искать определение слова «множество» не буду. Вроде бы интуитивно понятно что это. Множество это когда много чего-нибудь. В математике обычно имеют дело с множеством цифр. При этом цифры вовсе не обязаны быть рациональными – действительными, т.е с дробной частью. Может быть множество целых чисел. При этом их тоже бесконечно много. А может быть множество целых чисел от 0 до 100. Вполне себе множество из 99 цифр.
Часть американской элиты утверждает, что существует некое множество ценностей, которое является ценностями (т.е ценно) для всего человечества.
Значками это можно написать примерно так:

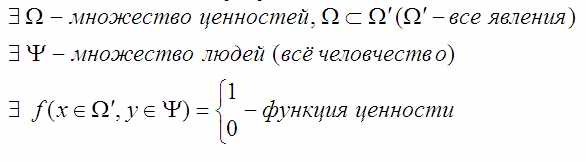
Т.е вначале я определяюсь с тем, что у меня вообще есть, о чём речь. Тут явно присутствуют некие ценные явления, точнее их множество Ω. Ещё тут есть люди, причём сразу всё человечество. Пусть это будет множеств Ψ. А ещё тут есть понятие ценности. Пусть это будет функция f(x,y) от явления и людей такая что если что-то ценно, то её значение равно 1, а если не ценно, то 0.
Ещё тут затесалось множество вообще всех явлений Ω’ в которое входят ценные явления Ω просто потому что как-то странно определять функцию f() на множестве только ценных явлений.
Так вот эти американцы думают, что:

… т.е то самое: всё, что входит в множество Ω ценно для вообще любого человека.
Ладно, пусть думают, что существует такое множество.
Но как-то странно множеству состоять только из одного явления, той самой пресловутой демократии. Тогда уж пусть аккуратно сформулируют список ценностей. Но я не видела даже попыток это сделать. Везде эти абстрактные ценностей и то самое утверждение, что они просто есть.
А раз так, то без этого чёткого списка утверждать то, что утверждает ЦРУшник это делать примерно так:

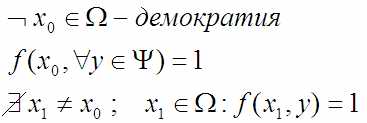
Пусть существует эта демократия X0, для которой всё в порядке, но не существует не равного ей X1 из того же множества Ω для которого выполнено то же самое. Очень странно, что страна юристов так и не придумала  список ценностей, но раз списка нет, то это равносильно утверждению, что демократия является единственной ценностью, а множество явлений без неё это пустое множество:

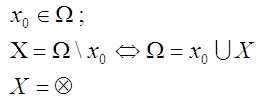
Определяется множество X как множество Ω без X0. Раз так, что множество Ω это их объединение (утверждения равносильны). Так вот это X – пустое множество, множество в котором ничего нет.
Множественному числу слова «values» это во всяком случае противоречит.