Перемещение жидкости (буквы и формулы)

Всё-таки имеет смысл порисовать трёхмерные картинки. Без них тоже можно, но лучше с ними. Всё взято отсюда:
http://akostina76.ucoz.ru/load/2-1-0-96

Пусть у жидкости или газа есть какой-то параметр. Пусть он будет называться A. Это может быть p – давление, T – температура и прочее. Но это всё не обязано быть одинаково во всех точках. Значит A = A(x,y,z), т.е зависит от трёх координат пространства. Постоянно по времени оно тоже не обязано быть. Значит A=A(x,y,z,t). Если рассматривать какой-то процесс, то он тоже развивается во времени. А это означает, что разнообразные молекулы могут перемещаться в пространстве, т.е координаты x,y,z это тоже функции от времени t. Значит так:
A=A(x(t),y(t),z(t),t)
А это означает, что полный дифференциал (т.е изменение по времени, которое обычно и берётся в законах сохранения) вычисляется так:


v_x, v_y, v_z  - стандартные обозначения скоростей. А выше нет ничего кроме правила дифференцирования сложной функции.
Картинки ниже будут на чёрном фоне потому что, как выяснилось, на нём видно больше различных цветов (жёлтый, например, на белом видно плохо).
Здесь:

… у меня нарисован некий произвольный объем жидкости и полный набор величин, который с ним связан.
Пусть в этом произвольном объеме несть две не менее произвольные точки A и B. Каждая из этих точек имеет свои координаты. Координаты A={x,y.z}. Пусть точка B отдалена от A на вектор ρ, чей размер {ξ,η, θ}. Тогда координаты точки B={x+ξ,y+η.z+θ}.
Пусть через некоторое время это объем куда-то переместился, как-то развернулся и как-то растянулся и сжался, т.е получилось так:

Чтобы проще было рисовать размеры, я его временно перемещу в начальную точку оставив деформации и повороты:

При деформациях расстояние между точками ρ поменялось и стало ρ’ (=ρ1). Изменения же по отдельным осям обозначены через {dξ , dη, dθ }.
Перемещение точек A и B можно вывести через вектора скоростей:

Любое перемещение S = V*t, где V – скорость, t – время. Здесь же перемещение точки A за время dt выражается через Va и равно Va*dt, перемещение точки B = Vb*dt.
Теперь всё то же самое в цифрах и векторах. Все векторы, которые есть при этом перемещении:

Просто функции с векторами:

У меня тут завелось два значения скорости в разных точках (V_a и V_b). Но логично предположить, что есть и вся прочая функция задающая скорости и всех остальных точек, а эта пара только два её случайно выбранных значения, т.е:


Есть такая штука которая называется ряд Тейлора. Рады Фурье позволяли получать функцию очень близкую к тому, что в них засунуто. Слагаемыми были простые для всевозможных вычислений синусы и косинусы.
Ряд Тейлора позволяет получать значение функции близкое к настоящему с какой-то точностью. В слагаемых фигурируют x в какой-то степени. Вот, например, разложение синуса:
taylor( sin(x), x=0, 7 );

Функция y=sin(x) очень похожа на функцию y=x возле нуля. Правда потом сходство пропадает. Но можно чуть увеличить точность если вычесть из x значение x^3/6. Графики выглядят так:
plot([sin(x),x,x-x^3/6],x=0..Pi/2,color=[red,blue,magenta]);

Обычно считается что объем (все расстояния) достаточно мал чтобы для приближения использовать только первое слагаемое разложения в ряд Тейлора.
Общая формула разложения в ряд Тейлора:

… Точнее в данном случае интересует второе слагаемое, выражаемое через первую производную потому, что dρ=(V_b-V_a)*dt, а первое слагаемое разложения V_b = V_a.
А вот второе слагаемое даст такое выражение:

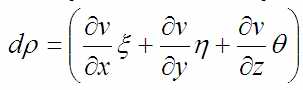
На картинке с синусами выше видно насколько мало отличается изменение синуса в окрестности нуля от изменения функции y=x. Их приращения (т.е те самые изменения функций) примерно равны. Это по сути аппроксимация (приближение) функции линейной функцией, заданной через угол наклона (=значение производной) в начальной точке. Тоже самое происходит и в формуле для dρ. Только этот метод использован сразу для трёх координат.
Последнее выражение хорошо короткой записью. Но ведь в меня не одна цифра, а целые вектора, т.е:

Это всё конкретные функции и конкретные значения, потому интересно как эти конкретные вещи выражаются друг через друга. Вот так они выражаются (роспись на проекции на оси X,Y,Z):

Это я про то насколько много функций возникает в трёхмерном случае, хотя это обычные функции, которые можно изобразить на отдельных двухмерных графиках. А итоговое трёхмерное движение даётся их объединением.