Скорость и высота волны в океане
Закон сохранения массы для несжимаемой жидкости записывается так: div(v)=0:
http://akostina76.ucoz.ru/blog/2017-04-08-4033
Ничего не мешает мне проинтегрировать это выражение по координате z. Ведь интеграл от нуля нулём и останется, т.е равенство будет сохранено:
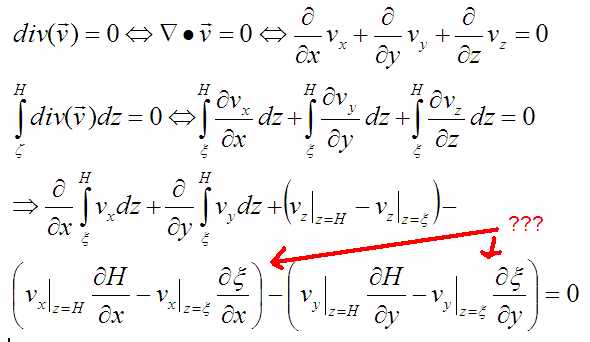
Откуда взялось два последних слагаемых, я не поняла. Самое неприятное, что там, скорее всего, что-то примитивное уровня интегральной арифметики, но что именно мне не сообразить.
Примерно также как и в случае модели струны:
http://akostina76.ucoz.ru/blog/2017-03-18-3962
… можно считать, что есть только вертикальная составляющая колебаний (т.е только вдоль оси Z – вверх и вниз). Это означает, что на изменение по этой оси Z уходят все изменения функции φ, которые при этом не перестают быть полным дифференциалом функции, вычисляемым по известной формуле:
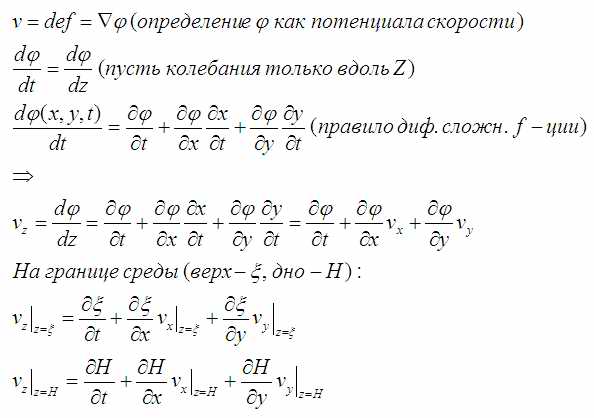
Если полученные значения на границах подставить в то, что получилось в интеграле от дивергенции, то почти всё сократится:

Равенства можно не только интегрировать по чему угодно но и дифференцировать. Полученное (без потери равенства) можно продифференцировать по времени t:
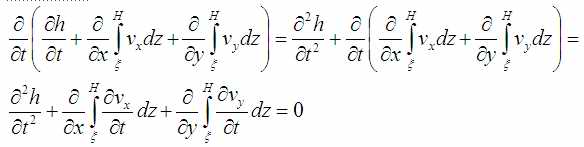
(Дифференцирование можно вносить по интеграл, менять местами и т.д. От перестановки мест тут ничего не меняется примерно как и тут: a+b+c+d=a+d+c+b).
Далее утверждается, что:
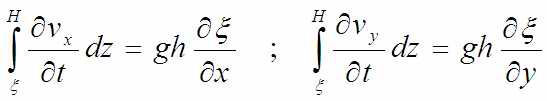
Почему оно так, я тоже не знаю. Разве что h =H-ξ явно вылезло из замены интеграла по этому промежутку на сам промежуток (h) умноженный на примерно постоянную на нём функцию.
Если это всё подставить, то получится так:

Это пока ещё не волновое уравнение, но нечто на него очень похожее. Тут есть вторые производные по времени и координатам (x,y) и нечто, претендующее на роль скорости волны.
Пусть скорость волны:
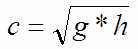
g – ускорение свободного паления, т.е константа. h – глубина в конкретном месте. Это, конечно, но константа, а некий параметр определяющий скорость волны при конкретной глубине. Поняв, что скорость зависит от глубины, можно избавиться от глубины (h), вспомнив, что рельеф дна со временем не меняется:
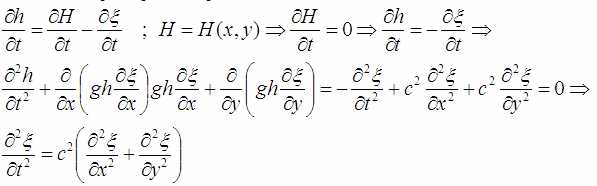
А это уже классический вариант волнового уравнения. Единственное что у него скорость «c» не совсем константа.
Раз процесс описывается волновым уравнением, то для него справедливо всё, что справедливо для волновых уравнений. В том числе «с» - это именно скорость перемещения волны (вместе с кинетической энергией, которую она несёт).
Кинетическая энергия = m*V*V/2, где V-скорость, m – масса. При подходе к берегу скорость снижается сильно (из-за уменьшения глубины), а энергия почти не меняется. Отсюда и рост массы (высоты волны) при подходе к берегу (вроде бы )) ).
|









