Уравнения и начальные и граничные условия для волн
Здесь было про закон сохранения массы:
http://akostina76.ucoz.ru/blog/2017-04-08-4033
… иногда называемый уравнением неразрывности.
Здесь было про закон сохранения энергии:
http://akostina76.ucoz.ru/blog/2017-04-09-4034
Ещё в механике есть понятие «импульс»:
Импульс
P=m*V, где P-импульс, m – масса, V – скорость.
Но поскольку основным методом являются законы сохранения или изменения каких-то интуитивно понятных количеств понятие «импульс» заменено на словосочетание «количество движения».
А коллекцию законов для газа/жидкости пополнил «закон количества движения», про который тут:
http://akostina76.ucoz.ru/load/2-1-0-96
Количество движения (по определению) это вот это:

… Если приглядеться, то видно что это всё тот же импульс, потому что v – это скорость, ρ – плотность, а тройной интеграл всего этого по объему τ даёт тот самый объем, умножение которого на плотность даёт массу m.
Количество движения как и прочие количества может изменяться за счёт внешних воздействий. В данном случае что-то может воздействовать на весть объем (например, сила тяжести) или на поверхность (например, просто сила, которая толкает в какую-то точку поверхности).
Вместе это записывается так:

… где F_m – силы, действующие на объем (M), а F_s – силы, действующие на поверхность тела (S).
Ещё можно так всё это записать:

Двойной интеграл по S в отличие от тройного по τ означает, что интегрирование идёт по двухмерной поверхности а не по трёхмерному объему.
Дальнейший вывод уравнений взят отсюда:
http://akostina76.ucoz.ru/load/2-1-0-98
У воды есть всякие разные параметры. Давление p, плотность ρ, скорость течения v (причем это вектор потому что течь вода может сразу в трёх измерениях). Все эти величины могут быть составными. Например давление в толще воды «p» это сумма атмосферного давления и давления, вызванного, например, подводным землетрясением (p’):

При это понятно что обычно всё меняется довольно плавно, т.е изменение обычной составляющей давления (выраженной градиентом, про которые было тут:
http://akostina76.ucoz.ru/blog/2017-04-08-4033
)… значительно меньше изменений дополнительного давления, которого до какого-то момента вообще не было, потом оно возникло и столь же быстро исчезло. Время действия этого дополнительного движения (t_w) мало.
Закон количества движения для этой задачи записывается так:

То, что выше – уравнение. С двумя его частями можно сделать что угодно. Равенство от этого никуда не денется. Можно, например, применить к ним оператор div. Будет так:

Тут появился ещё один оператор (Δ). Это оператор Лапласа, применяющий двойное дифференцирование (определение def дано выше). Про всё про это, включая то, что во что преобразуется тут:
Набла, grad, div, rot
Полный вид уравнения неразрывности (закон сохранения массы) такой:
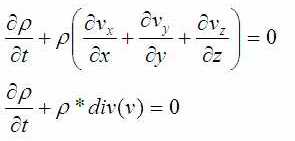
Но можно предположить, что жидкость несжимаема. Это означает, что её плотность не меняется со временем. В формулах это означает, что ρ не зависит от t (т.е не является функцией от t), а производная по t равна нулю:

Но это верно для всех V и даже V_0. Значит полученное выше уравнение количества движения (от которого взят div) можно и нужно приравнять к нулю:

То, что описывается – придуманная модель происходящего. Предположили, например, что жидкость несжимаема, т.е она конечно сжимаема но плотность меняется слишком мало, значит модель, в которой эти изменения вообще не учитываются, будет давать похожий на реальность результат.
Точно также можно предположить, что в модели действуют только так называемые потенциальные силы:
Консервативные силы
Самый яркий их пример – сила тяжести. Но важно не это а то, что потенциальные силы просто по определению это силы, обладающие потенциалом. Т. е для любой такой силы F есть некий потенциал U, для которого верно такое: F = grad(U).
Эти предположения обычно на чём-то основаны. В данном случае можно предположить, что жидкость обладает потенциалом скорости φ. Тогда можно записать так:

Но раз так, то можно это всё подставить в закон количества движения и убрать из него градиенты (Набла = grad):

Можно получить чуть другой вид для закона сохранения массы (т. е и его выразить через потенциал φ):
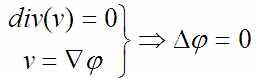
А закон сохранения энергии для всё того же потенциала φ записывается в виде интеграла Лагранжа-Коши:
Интеграл Лагранжа-Коши
… который для этого случая имеет вид:

Получилась система из двух уравнений с неизвестной функцией φ.
К любым дифференциальным уравнениям полагаются начальные (т.е в начальный момент времени) и граничные (т.е на концах объекта) условия.
В данном случае среда, в которой что-то происходит, это вода между дном и верхней кромкой:
plot3d({0.1*x,2+0.2*sin(x*y)},x=0..6,y=0..6,axes=boxed,scaling=constrained);

Форма дна задаётся некой функцией z=H(x,y), т.е его глубина не постоянна (значение функции не одинаково для разных x,y), но его форма не меняется со временем, потому H не зависит от t.
А вот верхняя кромка z=ξ(x,y,t) может меняться со временем. Это - свободная поверхность.
Первое граничное условие – равенство давления на поверхности атмосферному давлению:
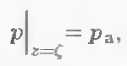
Второе граничное условие – непротекание дня:

Течения могут быть какие угодно, но вот скорость втекания в дно на поверхности дна строго нулевая (n – вектор нормали к поверхности, т.е вектора перпендикулярного к ней).
Не поняла почему, но утверждается что так:

Но если второе (w=) подставить в первое (gξ=) то граничное условие на поверхности перепишется в виде:
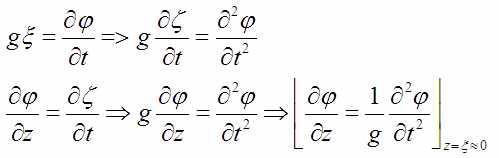
Начальные условия:

|









