Векторы как инструмент

Тут:
http://akostina76.ucoz.ru/blog/2017-02-09-3836

… было про объект несколько условно названный струной. Струна может быть довольно толстой балкой. Главное чтобы все смещения в ней были по одной оси X. Все остальные конечно тоже могут быть, но они должны быть слишком малы чтобы их учитывать. Именно в этой ситуации реальный физический объект можно заменить его одномерной (с одной осью X) моделью. И только в  этом случае для описания происходящего достаточно одной классической цифры. Цифра может быть отрицательной и положительной, обозначая например сдвиг вправо и влево, но цифра только одна.
В общем случае исходный «кубик» (на самом деле любая малая область):

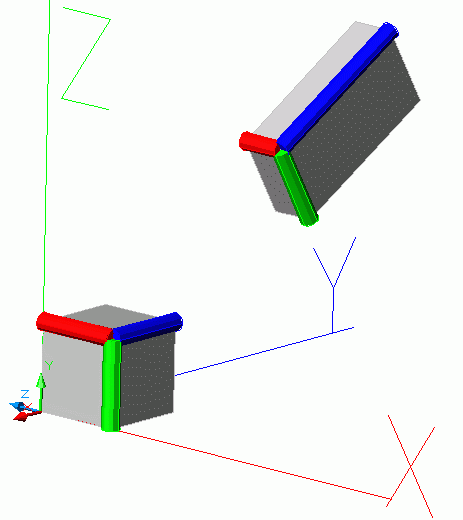
… может не только перемеситься на любое расстояние по трём координатам, но и продеформироваться на разные величины (по этим осям) и даже как-то развернуться.
Вектор это комбинация из нескольких цифр. В случае координат трёхмерного пространства этих цифр три. Например, кубик переместился от исходного положения по оси X на 15, по Y и Z на 20. Это всё можно обозначить вектором перемещения:

W=(15,20,20).
Точно также можно записать, что по оси X произошло сжатие в 2 раза, по оси Y растяжение в 2 раза, а размер по оси Z не изменился. Получится вектор (0.5,2,1).
Но просто набор трёх цифр это не очень аккуратно. Всё-таки здесь полноценное пространство потому логично обзавестись комбинацией из трёх единичных векторов, задающих направления по осям:

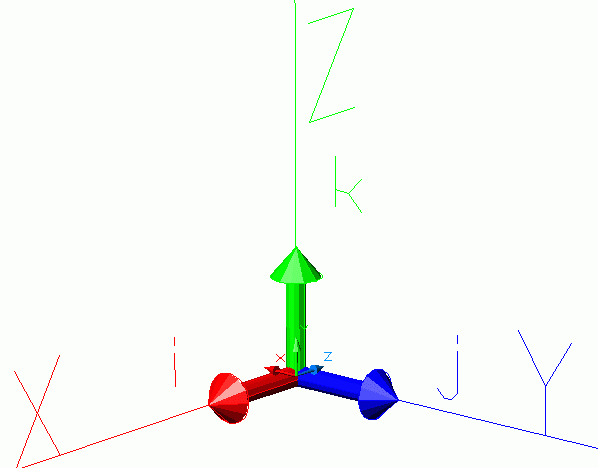
И тогда комбинация цифр будет означать, на сколько надо умножить каждый единичный вектор чтобы получить итоговый вектор.
Обычно вектора обозначаются стрелкой сверху, но часто её не рисуют:

Обычно приходится иметь дело не только с простым перемещением но и с деформациями потому кроме стандартной комбинации единичных векторов (i,j,k) обзавелись так называемым оператором Набла, или grad.
Различные обозначения:

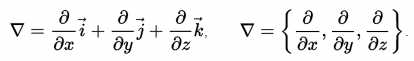
Полное название этой штуки «векторный дифференциальный оператор». Во-первых, в нем содержатся единичные вектора (i,j,k), потому он векторный. Во-вторых, это оператор, т.е эта штука проделывает некую операцию с тем, что ей подсовывают. В каком-то смысле это примерно тоже, что умножение например на два или возведение в степень, т.е любая функция. В-третьих это дифференциальный оператор, т.е занимается он дифференцированием.
Если приложить этот оператор в некой функции φ(x,y,z), то получится так:

Это вектор, т.е нечто в трёх координатах (X,Y,Z) и означающее например те самые деформации кубика по всем осям.
С векторами как и с числами можно выполнять различные операции. Но кроме привычных сложений, вычитаний вектора можно умножать, причем скалярно и векторно.
Здесь действуют примерно такие же правила как при делении в столбик.  Просто есть правило, указывающее, что надо делать чтобы получить результат называемый скалярным произведением.
Вот оно:

В результате получается уже не вектор а скаляр, т.е обычное число, полученное из коэффициентов при единичных векторах.
Если скалярно умножить вектор grad на какой-то другой вектор, то получится так:

Полученный скаляр называется дивергенцией вектора «a».
Эти операторы используются для сокращённой записи различных законов.
Например, закон сохранения массы означает, что как бы не перемещался, деформировался и крутился некий объем вещества dτ, количество молекул а нём (в штуках), т.е масса, не изменится.
Можно это записать так:

Три интеграла означают только то, что объем кубика это произведение трёх размеров X(№1)*Y(№2)*Z(№3). Этот объем и умножается на плотность ρ чтобы получить ту самую неизменную массу. В случае кубика объем можно посчитать умножением. При более сложных фигурах требуются интегралы.
Выше – запись закона сохранения массы в интегральной форме. Но можно записать и в дифференциальной. Для этого надо внести дифференцирование по времени внутрь всех этих интегралов.
Не вдаваясь в подробности почему это так (по выведенной математической формуле, не имеющей отношения в механике):

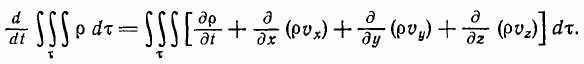
Причём по закону сохранения массы это должно быть равно нулю при любом объеме. А это так только если равно нулю само подинтегральное выражение.
К тому же в данном случае вводится так называемая гипотеза сплошной среды, означающая что плотность ρ одинакова во всех точках исследуемого объема, а значит не зависит от x,y,z. А раз так её (как «константу») можно вытащить из-под всех дифференциалов: