Закон сохранения энергии

Взято отсюда:
http://akostina76.ucoz.ru/load/2-1-0-96

Про закон сохранения массы было тут:
http://akostina76.ucoz.ru/blog/2017-04-08-4033

Физический закон это то, что действует в изучаемой системе. Всё происходящее объясняется именно этими законами. Только результаты действия этих законов в каждом конкретном случае будут разные, иногда неожиданные.
Другой закон сохранения, представляющий особый интерес, – закон сохранения энергии. Законы называются «законами сохранения» довольно условно. Про это было тут:
https://www.facebook.com/notes/904925662906333

… Т.е и масса и энергия, конечно могут меняться за счёт притока извне и оттока туда же.
Название «закон сохранения» берётся из случай, когда таких притоков и оттоков не было, что можно записать как «свойство A=const» или «dA/dt = 0» (т.е изменение свойства A равно нулю).
Полная энергия системы состоит и кинетической и внутренней энергии. Пусть она, действительно, не меняется. Тогда это можно записать так:

Внутренняя (потенциальная) энергия равна количеству этой энергии в единице объема (что-то вроде плотности энергии) умноженной на весь объём:

Значение E для материала обычно известно из экспериментов и моделей. Например для идеального газа, поведение которого описывается уравнением Клайперона (p=ρRT)  можно его вычислить так:

Кинетическая энергия массы M, движущейся со скоростью V: T=M*V*V/2. Но поскольку тут тоже речь идёт о неком неизвестном предмете неизвестной формы это тоже записывается через интеграл по объему:

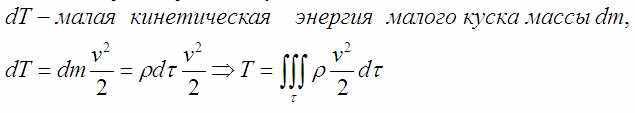
Если подставить всё это в закон сохранения энергии, то будет так:

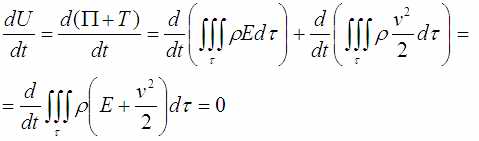
Эффект цунами вызван именно этим законом сохранения энергии. В какой-то момент дно на большой глубине «подпрыгивает» и приводит в движение 4 км воды над собой, (поднимая и роняя её). Эта энергия возникает в механической системе и никуда не девается. Она только перемещается вместе с волной в сторону от эпицентра.
Выше выведен общий случай уравнения закона сохранения энергии. Его форма немного меняется при конкретных случаях газа/жидкости.
Например в случае идеальной (т.е без внутреннего трения), несжимаемой (т.е плотность ρ не зависит от времени) жидкости находящейся под действием сил тяжести интегральный вариант (т.е U=П+T=const) принимает вид Закона Бернулли:
:
:Закон сохранения энергии – частный случай второго закона Ньютона.