Задачи математического анализа

Отчасти этот текст:
http://akostina76.ucoz.ru/blog/2017-04-20-4066

… продолжение темы того, что люди не знают, чем отличается 1/3 от 30%. Я тогда подумала, что я тоже не знаю, чем отличаются примерно одинаковые константы. Тоже самое с корнями квадратного уравнения. Синусы при обсчёте углов используются сплошь и рядом. А где могут быть столь необходимы координаты пересечения этой несчастной параболы с осью X сходу не вспомнить. Это надо знать, чтобы ночью разбудили и от зубов отскакивало? А зачем надо меня ночью будить с этим вопросом?
То, что написано выше только отчасти шутка. Нет ответов на эти вопросы, если они висят в воздухе и не являются частями конкретной задачи.
При исследовании функции мне действительно потребовались корни квадратного уравнения просто потому, что уход функции на бесконечность при делении на ноль это действительно важно. Это важно хотя бы для того чтобы выбрать интервал в котором компьютер нарисует эту функцию не запутавшись в бесконечных масштабах.
И точное значении Пи мне в данном случае потребовалось как и точное значение корня из 5. Просто не повезло. На правом конце параболы эти значения подошли слишком близко и от того, что из них больше принципиально зависел вид функции. Это тот конкретный случай, когда было важно то отличие 10+sqrt(5) от 4*Пи которое не на много больше чем отличие 30% от 1/3. А вот слева этой точности не потребовалось.
Если хочется потренировать голову, то есть и другие задачи математического анализа, которые можно «покрутить в голове и руках».
В примере с видом функции мне довольно легко удалось понять, как ведёт себя функция на бесконечности. Синус (=1) делённый на квадрат бесконечного X очевидно стремился к нулю.
Бывают случаи, когда поведение функции в какой-то точке не столь очевидно. Тогда приходится вычислять значение предела функции в некой точке:

4-й пример отсюда:
http://www.matburo.ru/ex_ma.php?p1=mapred

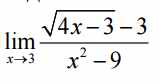
Если просто подставить в функцию конкретное значение, то получится 0 делить на 0 и непонятно, ноль это (потому, что делят ноль), бесконечность (потому, что делят на ноль) или какая-то константа потому что эти нули друг друга как-то компенсируют:

Но чуть-чуть покрутив выражение функции всё-таки можно получить то значение, к которому на бесконечности стремиться эта функция:
Здесь:
http://akostina76.ucoz.ru/blog/2017-02-12-3846

… всё началось с удачной замены переменных а надежде, что исходное выражение придёт к виду, по которому что-то будет понятно. Замена переменных была удачной. Именно поэтому действительно получилось. Точно также придётся «покрутить в руках» и эту функцию. А что будет, если умножить числитель и знаменатель на выражение, которое позволит избавиться от корня сверху?:

Вот уже что-то и получилось, т.е «выбилось» их этого выражения нечто, которое можно сократить. Сверху возникло (x-3) а снизу есть (x*x-9)=(x-3)*(x+3):

А что теперь получилось? Не исчезла ли эта неопределённость в виде нуля делённого на ноль? Уже понятно, что исчезла. Можно смело опять подставить в функцию значение x=3:

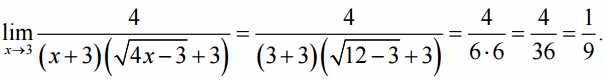
Т.е при x=3 функция стремиться к 1/9.
Есть «жульнический» способ решения пределов. Довольно часто предел можно оттейлорить (т.е разложить в ряд Тейлора, про который было тут:
http://akostina76.ucoz.ru/blog/2017-04-16-4059

… и получить «степени нулей» в числителе на знаменателе). Например, одна из самых известных неопределённостей такая:

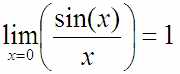
Теперь-то строго доказано, что это равно 1, но там тоже те самые два нуля, которые делятся друг на друга. Доказать это можно по-разному. Особо повеселил этот вариант:
https://math24.biz/limit

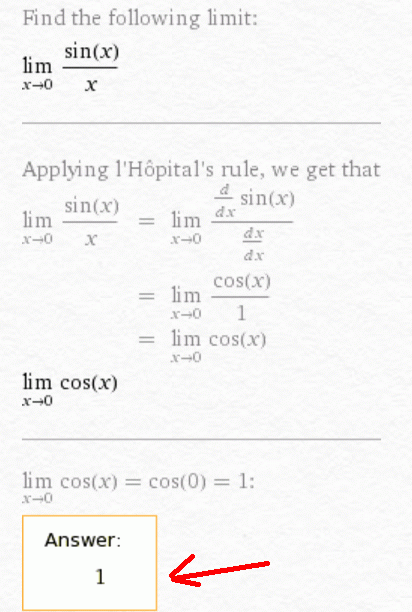
… который и есть то самое разложение в ряд Тейлора, которое (как и все остальные методы) работает не всегда но довольно часто. Но есть случаи, когда эта довольно универсальная «отвертка» не работает и требуется какая-то изворотливость при поиске решения.
Точно также можно поиграться с интегралами. В примерах здесь:
http://www.matburo.ru/ex_ma.php?p1=maint

… я уже не очень понимаю, что делается. Но подинтегральное выражение тоже надо как-то «покрутить в руках» чтобы получить что-то, что уже легко интегрируется. Ряд Фурье – не зря разложение по синусам и косинусам. Интеграл синуса – косинус, интеграл косинуса – синус. И прочие выражения надо привести к тому виду, который легко интегрируется.
Здесь, например, мне потребовались формулы тригонометрических преобразований:
http://akostina76.ucoz.ru/blog/2017-03-10-3936

Точно также произведение синусов проинтегрировать невозможно, но вот если преобразовать его воспользовавшись тригонометрической формулой то запросто:

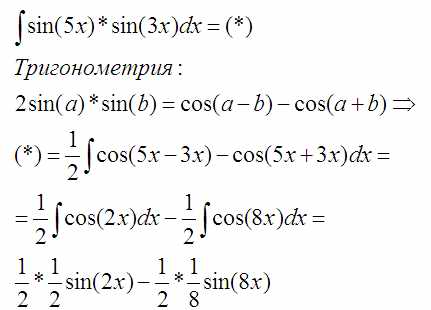
Примерно так это здесь:
https://math24.biz/integral

… и решается.